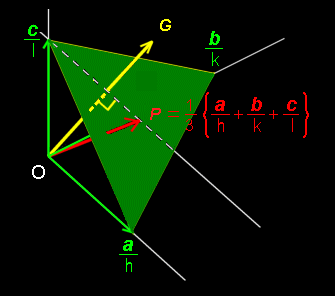
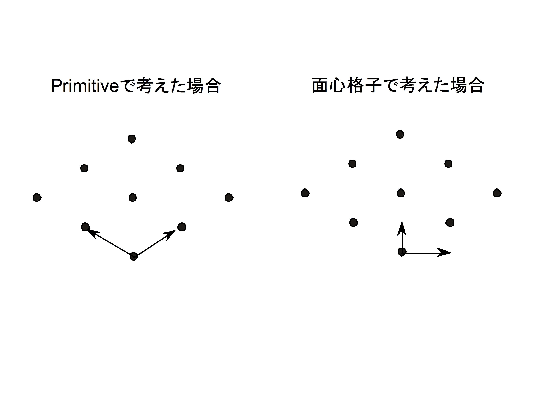
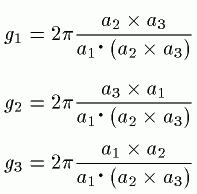逆格子空間

逆格子空間（ぎゃくこうしくうかん、英: reciprocal space）は逆格子ベクトルによって構成される空間のこと。実空間の周期性が反映される。逆空間、運動量空間、波数空間、k空間と言うこともある。

実空間と逆格子空間の関係は数学的にはフーリエ変換そのものであり、格子たとえば結晶の周期性を見ることができる。また物理的には位置と運動量、あるいは位置と波数の関係になっている。

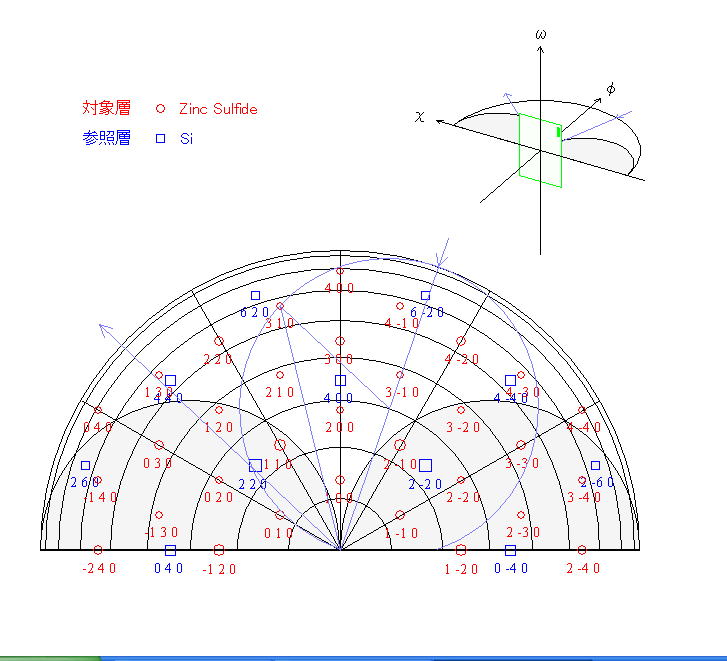
光やX線の散乱は固体の結晶面の間隔とブラッグの法則で決まるが、逆格子空間を使うと便利なことがある。たとえば逆格子点の位置に光の強め合うスポットができるなど。

また固体中の電子の動きを見る場合、重要なのは位置よりも運動量の二乗に比例するエネルギーであるため、固体物理学での逆格子空間の用途は広い。

結晶では原子の周期的配列による並進対称性のため、一電子の固有関数(ブロッホ関数)、結晶格子の基準振動、そのほかの集団運動のモードなどが全て、波数で指定される平面波 $e^{i\mathbf {k} \cdot \mathbf {r} }$ に似た形を持ち、対応するエネルギーまたは振動数も波数についての関数であるため、波数空間は特に重要な意味を持つ。バンド理論では、ポテンシャルの周期性の影響を調べるのに逆格子空間を用いると便利である。

関連項目